多目标优化 |
您所在的位置:网站首页 › matlab 叠图 › 多目标优化 |
多目标优化
|
今天为各位讲解多目标优化算法NSGA-Ⅲ,实际上我们分别在NSGA-II多目标优化算法讲解(附MATLAB代码)、多目标优化 | 基于NSGA-II的多目标0-1背包问题求解(附matlab代码)、多目标优化 | NSGA-II进阶教程(全网首个三目标优化教程)这几篇推文中对NSGA-Ⅱ做了详细讲解。 那今天讲解的NSGA-Ⅲ实际上和NSGA-Ⅱ只是在选择机制上有区别,其他步骤完全相同。因此,需要各位先回顾一下NSGA-Ⅱ的基本步骤。 在这里,还有一个基本问题需要各位注意一下,NSGA-Ⅱ是multi-objective优化,即多目标优化,而NSGA-Ⅲ的many-objective优化,即超多目标优化。其中,multi-objective(多目标)指的是2或3个优化目标,many-objective(超多目标)指的是至少4个优化目标。 因此,NSGA-Ⅲ的优势是求解超多目标优化问题,即4个及以上的多目标优化问题。 ※注:由于NSGA-Ⅲ内容较多,所以将这部分内容讲解分成三篇推文讲解。 目录 NSGA-Ⅱ求解步骤回顾NSGA-Ⅲ算法设计思路NSGA-Ⅲ代码获取方式参考文献NSGA-Ⅱ求解步骤回顾遗传算法GA伪代码无论是NSGA-Ⅱ,还是NSGA-Ⅲ,它们的基础都是遗传算法GA。GA的伪代码如下:  GA的基本思路为,种群初始化→进入主循环→选择操作→交叉操作→变异操作→种群更新操作→输出全局最优解。 NSGA-Ⅱ整体伪代码在了解了GA的基本思路后,再来看一下NSGA-Ⅱ的基本思路:  NSGA-Ⅱ与GA的一大差异在于个体的选择机制。 GA是通过轮盘赌选择或锦标赛选择等选择方式,从父代种群(种群数目为 而NSGA-Ⅱ先将父代种群 其中,快速非支配排序  NSGA-Ⅱ拥挤度距离计算伪代码 NSGA-Ⅱ拥挤度距离计算伪代码拥挤度距离计算 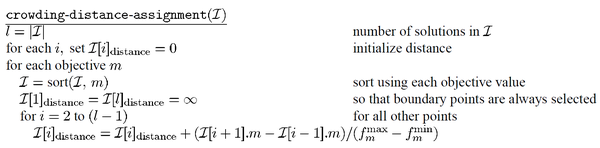 NSGA-Ⅱ示意图 NSGA-Ⅱ示意图NSGA-Ⅱ核心步骤示意图如下图所示:  NSGA-Ⅲ算法设计思路 NSGA-Ⅲ算法设计思路在回顾完NSGA-Ⅱ之后,我们开始今天的主题——NSGA-Ⅲ。实际上,在文章的开篇我们已经提到过,NSGA-Ⅲ与NSGA-Ⅱ的唯一差别在于选择机制。再严格一点,可以说是摒弃拥挤度距离排序机制,而采用一种基于参考点排序的新机制。  NSGA-Ⅲ整体伪代码 NSGA-Ⅲ整体伪代码我们先给出NSGA-Ⅲ伪代码:  细心的同学已经发现,NSGA-Ⅲ的伪代码实际上和NSGA-Ⅱ的伪代码基本一致,下面我们将这两个伪代码进行对比:  左侧NSGA-Ⅲ标红的地方和右侧NSGA-Ⅱ标红的地方就是两者的差异,即两者的选择机制不同。其它步骤则完全相同。 从选择机制的伪代码行数可以看出,NSGA-Ⅲ的选择机制更为复杂,接下来则重点剖析一下NSGA-Ⅲ的选择机制。 首先需要明确一个问题,如果在进行快速非支配排序后,前 因此,后续基于参考点排序是建立在一个前提之上,即前 既然,NSGA-Ⅲ采用一种基于参考点的排序机制,那么就有3个很直接的问题: 这些参考点究竟是什么? 采用这种基于参考点的排序机制优势在哪里? 如何生成这些参考点?首先回答第一个问题——这些参考点究竟是什么。 以一个三目标问题为例,这些参考点实际上等间距均匀分布在一个等边三角形平面上,其中这个等边三角形的三个顶点坐标分别为(1,0,0),(0,1,0),(0,0,1),则这些参考点的示意图如下图所示,其中下图中的15个小黑点就是参考点:  接下来回答第二个问题——采用这种基于参考点的排序机制优势在哪里。 我们都希望多目标优化最终获得的帕列托解能够尽可能均匀分布,而不是这里一堆解,那里一堆解。 因为,均匀分布的帕列托解可以为用户提供多个平衡的解决方案,这些解都保留各自的优势。而分块密集的帕列托解很明显不利于用户做决策,很明显只有这几块的解是能够支撑用户决策的,而缺少其它位置的平衡解,显示不是我们多目标优化的初衷。 因此,为了使最终获得的帕列托解能够均匀分布,NSGA-Ⅲ采用基于参考点排序的方式,在解与参考点之间建立联系,因为构造的参考点是均匀分布的,所以我们希望最终生成的帕列托解也可以保持均匀分布的这一特性。 最后回到第三个问题——如何生成这些参考点。 我们先回到第一个问题的那张图,各位要注意一点,这些参考点是等间距分布的。  示意图中的参考点是4等分分布的,这些参考点的几何生成方法如下: 先将3个顶点(即(1,0,0),(0,1,0),(0,0,1))进行连线,形成等边三角形。在每条边上进行4等分操作,即每条边各有5个等分点,这些等分点为部分参考点。将与各边平行的各对等分点连线,连线产生的交点为另一部分参考点。上述交点全集即为生成的参考点。上述参考点生成方式是以3目标为例,4目标及以上的参考点生成方法可以此类推。3目标4等分所生成的参考点示意图如下图所示。  各位可以发现,如果目标数目为 还是以上述3目标4等分为例,参考点的代数生成方法如下图所示:  4目标5等分的代数生成方法如下图所示:  参考点生成MATLAB代码如下: function [W,N] = UniformPoint(N,M) %UniformPoint - Generate a set of uniformly distributed points on the unit %hyperplane % % [W,N] = UniformPoint(N,M) returns approximate N uniformly distributed % points with M objectives. % % Example: % [W,N] = UniformPoint(275,10) %-------------------------------------------------------------------------- % Copyright (c) 2016-2017 BIMK Group. You are free to use the PlatEMO for % research purposes. All publications which use this platform or any code % in the platform should acknowledge the use of "PlatEMO" and reference "Ye % Tian, Ran Cheng, Xingyi Zhang, and Yaochu Jin, PlatEMO: A MATLAB Platform % for Evolutionary Multi-Objective Optimization [Educational Forum], IEEE % Computational Intelligence Magazine, 2017, 12(4): 73-87". %-------------------------------------------------------------------------- H1 = 1; while nchoosek(H1+M,M-1) |
【本文地址】
今日新闻 |
推荐新闻 |